Sean dos vectores  y
y  en el espacio vectorial
en el espacio vectorial  . El producto vectorial entre
. El producto vectorial entre  y
y  da como resultado un nuevo vector,
da como resultado un nuevo vector,  . El producto vectorial
. El producto vectorial  y
y  se denota mediante
se denota mediante  , por ello se lo llama también producto cruz. En los textos manuscritos, para evitar confusiones con la letra x (equis), es frecuente denotar el producto vectorial mediante:1
, por ello se lo llama también producto cruz. En los textos manuscritos, para evitar confusiones con la letra x (equis), es frecuente denotar el producto vectorial mediante:1
 y
y  en el espacio vectorial
en el espacio vectorial  . El producto vectorial entre
. El producto vectorial entre  y
y  da como resultado un nuevo vector,
da como resultado un nuevo vector,  . El producto vectorial
. El producto vectorial  y
y  se denota mediante
se denota mediante  , por ello se lo llama también producto cruz. En los textos manuscritos, para evitar confusiones con la letra x (equis), es frecuente denotar el producto vectorial mediante:1
, por ello se lo llama también producto cruz. En los textos manuscritos, para evitar confusiones con la letra x (equis), es frecuente denotar el producto vectorial mediante:1
El producto vectorial puede definirse de una manera más compacta de la siguiente manera:
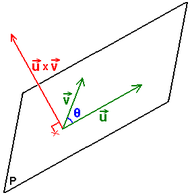
donde  es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorchos.
es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorchos.
 es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorchos.
es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorchos.Precisiones
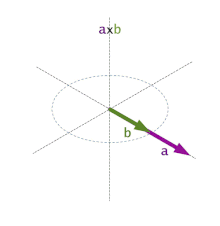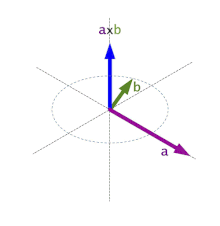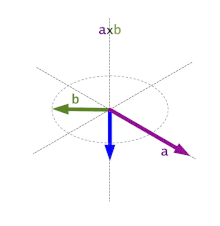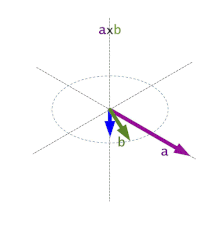
Se denomina producto vectorial del vector a por el vector b 2 al vector denotado por 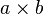 y definido por las tres exigencias siguientes:
y definido por las tres exigencias siguientes:
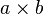 y definido por las tres exigencias siguientes:
y definido por las tres exigencias siguientes:- el módulo de
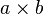 es igual al módulo de a por módulo de b por
es igual al módulo de a por módulo de b por  , en donde
, en donde  es el ángulo orientado formado por los vectores a y b
es el ángulo orientado formado por los vectores a y b - el vector
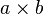 es perpendicular a cada uno de los vectores a y b
es perpendicular a cada uno de los vectores a y b - la dirección del vector
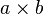 respecto a los vectores a y b es igual que la del eje coordenado Oz respecto a los ejes coordenados Ox y Oy, como si girase de Ox a Oy y avanzase en la dirección positiva de Oz.
respecto a los vectores a y b es igual que la del eje coordenado Oz respecto a los ejes coordenados Ox y Oy, como si girase de Ox a Oy y avanzase en la dirección positiva de Oz.
Producto vectorial de dos vectores
Sean los vectores concurrentes de  , el espacio afín tridimensional según la base anterior. Se define el producto:
, el espacio afín tridimensional según la base anterior. Se define el producto:
 , el espacio afín tridimensional según la base anterior. Se define el producto:
, el espacio afín tridimensional según la base anterior. Se define el producto:
Donde w es el producto vectorial de u y v, definido así:
donde la última fórmula se interpreta como:
esto es:
Usando una notación más compacta, mediante el desarrollo por la primera fila de un determinante simbólico de orden 3 (simbólico ya que los términos de la primera fila no son escalares):
Que da origen a la llamada regla de la mano derecha o regla del sacacorchos: girando el primer vector hacia el segundo por el ángulo más pequeño, la dirección de  es el de un sacacorchos que gire en la misma dirección.
es el de un sacacorchos que gire en la misma dirección.
 es el de un sacacorchos que gire en la misma dirección.
es el de un sacacorchos que gire en la misma dirección.Ejemplo
El producto vectorial de los vectores  y
y  se calcula del siguiente modo:
se calcula del siguiente modo:
 y
y  se calcula del siguiente modo:
se calcula del siguiente modo:
Expandiendo el determinante:
Dando como resultado:
Puede verificarse fácilmente que  es ortogonal a los vectores
es ortogonal a los vectores  y
y  efectuando el producto escalar y verificando que éste es nulo (condición de perpendicularidad de vectores)
efectuando el producto escalar y verificando que éste es nulo (condición de perpendicularidad de vectores)
 es ortogonal a los vectores
es ortogonal a los vectores  y
y  efectuando el producto escalar y verificando que éste es nulo (condición de perpendicularidad de vectores)
efectuando el producto escalar y verificando que éste es nulo (condición de perpendicularidad de vectores)





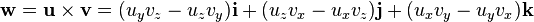







No hay comentarios:
Publicar un comentario