El espacio euclídeo es un tipo de espacio geométrico donde se satisfacen los axiomas de Euclides de la geometría. La recta real, el plano euclídeo y el espacio tridimensional de la geometría euclidiana son casos especiales de espacios euclídeos de dimensiones 1, 2 y 3 respectivamente. El concepto abstracto de espacio euclídeo generaliza esas construcciones a más dimensiones. Un espacio euclídeo es un espacio vectorial completo dotado de un producto interno (lo cual lo convierte además en un espacio normado, un espacio métrico y una variedad riemanniana al mismo tiempo).
El término euclídeo se utiliza para distinguir estos espacios de los espacios "curvos" de las geometrías no euclidianas y del espacio de la teoría de la relatividad de Einstein. Para resaltar el hecho de que un espacio euclídeo puede poseer n dimensiones, se suele hablar de "espacio euclídeo n-dimensional" (denotado  , o incluso
, o incluso 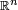 ).
).
 , o incluso
, o incluso 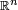 ).
).
Un espacio vectorial E, de dimensión n, se llama espacio vectorial euclídeo n-dimensional si en E se halla definido un producto escalar.
Ejemplo:
Para el espacio vectorial n-dimensional Rn se puede definir:
Que como fácilmente se comprueba se trata de un producto escalar, llamado producto escalar canónico.
No hay comentarios:
Publicar un comentario